主席树学习笔记

主席树学习笔记

主席树就是可持久化的线段树，可以轻松的访问历史版本
暴力的可持久化线段树就是每一次修改都重新把原来的线段树copy过来然后修改，复杂度爆炸
但线段树有一个优美的性质就是我们发现每次修改只会修改logn段区间，也就是说其他nlogn段区间可以直接copy上一个历史版本的区间位置
既然知道这个思想了，那我们就可以上图了(copy的毕竟不用修改(笑）图作者)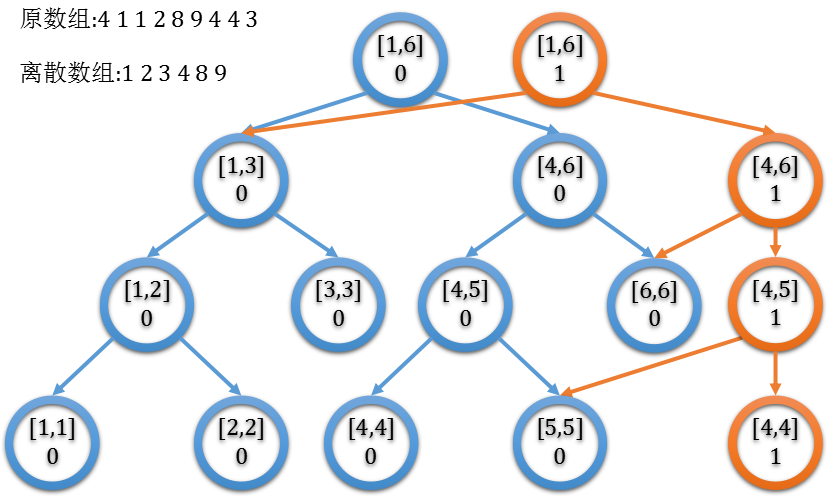

这样我们就成功的把一这个数字插进来了（狂喜）（这里的区间[l,r]指的事值在[l,r]之间的数有几个）

例题1

如题，给定N个整数构成的序列，将对于指定的闭区间查询其区间内的第K小值。
想必看到这样的题面，各位的内心一定事噔噔咚的⑧
我们考虑问题的简化版
区间一定事从1开始的且连续的
也就是说我们可以对区间排序然后离线做平衡树
但实际上我们可以在线用线段树做
我们对于每个[1,k] (1<=k<=n) 建一颗线段树
但显然每个区间之间只有1次修改，所以我们直接上主席树每次加一个点进去
对于区间[1,x]求第k大，我们只要像对平衡树一样左边小右边大，左边的数字个数如果小于k就往右边走，并且将k减去左边数字个数；左边比k打，则答案一定在左边 一直这样做直到k为0为止
那么现在区间的开头不是1了怎么办？显然的我们每个区间上需要记录的只是数字的个数而已，所以我们直接前缀和处理就好了[l,r]区间的值就是[1,r]-[1,l-1] (显然只要把查询的logn区间减一下就行（oi都学到这个地步了这点思想应该事有的⑧）)
分函数来康康

update

因为区间不是连续的，所以我们在存储线段树时，还要存贮他的两个儿子的下标

int update(int now,int l,int r,int k) //now时当前所在区间（历史版本的（准确的说事当前新区间所基于的那个历史版本））的下标 l,r字面意思 k就事要插入的数
{
    int mid=(l+r)>>1;
    int rt=++tot;//新建区间
    ch[rt][0]=ch[now][0];//直接copy左右区间
    ch[rt][1]=ch[now][1];
    sum[rt]=sum[now]+1;//不一样的是当前所搜索到的区间
    if(l<r)
    {
        if(k<=mid) ch[rt][0]=update(ch[now][0],l,mid,k); //接下来找的区间在左边 注意此时的新区间的有儿子要更新 已经不再是旧区间的左儿子了
        else ch[rt][1]=update(ch[now][1],mid+1,r,k);//接下来找的区间在右边 注意此时的新区间的有儿子要更新 已经不再是旧区间的右儿子了
    }
    return rt; //把区间的下标传回去，方便上面的操作
}

晕不？（不晕要么是大佬，要么是我讲的好）
学习主席树时要分清两个区间
一个是大区间，也就是我们维护问题本身所需要的维护的东西
例如本题我们的大区间就是[1,x] (1<=x<=n)中在小区间[l,r] 中的数有多少个
维护的大区间是问题的本质，小区间则是维护大区间的工具
（不知道这样会不会更绕）

query

int query(int u,int v,int l,int r,int k) //v是大区间[1,r]当前所访问到的小区间的下标 u则是[1,l-1]的
{
    int mid=(l+r)>>1;
    if(l==r) return l;
    int x=sum[ch[v][0]]-sum[ch[u][0]]; //求出所访问的大区间的当前小区间的值
    if(x>=k) return query(ch[u][0],ch[v][0],l,mid,k); //在左边
    else return query(ch[u][1],ch[v][1],mid+1,r,k-x); //在右边
}

完整程序

// luogu-judger-enable-o2
#include<bits/stdc++.h>
using namespace std;
const int N=200009,times=20;
int n,m,q,tot=0;
int a[N],b[N];
int t[N],sum[N*times],ch[N*times][2];
int build(int l,int r)
{
    int mid=(l+r)>>1;
    int rt=++tot;
    if(l<r)
    {
        ch[rt][0]=build(l,mid);
        ch[rt][1]=build(mid+1,r);
    }
    return rt;
}
int update(int now,int l,int r,int k)
{
    int mid=(l+r)>>1;
    int rt=++tot;
    ch[rt][0]=ch[now][0];
    ch[rt][1]=ch[now][1];
    sum[rt]=sum[now]+1;
    if(l<r)
    {
        if(k<=mid) ch[rt][0]=update(ch[now][0],l,mid,k);
        else ch[rt][1]=update(ch[now][1],mid+1,r,k);
    }
    return rt;
}
int query(int u,int v,int l,int r,int k)
{
    int mid=(l+r)>>1;
    if(l==r) return l;
    int x=sum[ch[v][0]]-sum[ch[u][0]];
    if(x>=k) return query(ch[u][0],ch[v][0],l,mid,k);
    else return query(ch[u][1],ch[v][1],mid+1,r,k-x);    
}
int main()
{
    int test=1;
    while(test--)
    {
        tot=0;
        memset(t,0,sizeof(t));
        memset(sum,0,sizeof(sum));
        memset(ch,0,sizeof(ch));
        scanf("%d %d",&n,&q);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            b[i]=a[i];
        }
        sort(b+1,b+n+1);
        m=unique(b+1,b+n+1)-b-1;
        t[0]=build(1,m);
        for(int i=1;i<=n;i++)
        {
            a[i]=lower_bound(b+1,b+1+m,a[i])-b;
            t[i]=update(t[i-1],1,m,a[i]);    
        }
        for(int i=1,x,y,z;i<=q;i++)
        {
            scanf("%d%d%d",&x,&y,&z);
            int p=query(t[x-1],t[y],1,m,z);
            printf("%d\n",b[p]);
        }
    }
}

例题2 luogu P3168 [CQOI2015]任务查询系统

先把那个奇怪的求和扔到一遍，只是个裸的区间修改线段树
现在我们原本是单点修改变成了区间修改，怎么办呢？把一个区间分成好几个点插入肯定超时的鸭（所以我们可以把区间分块）
我们发现，本题只要做单点查询就好了，所以差分就阔以了
那么单点查询就是求差分数组的前缀和，那么对于每个历史版本我们只要更新两个差分数组即可
把模板改很多就好了