题解 P4374 【[USACO18OPEN]Disruption】

既然没有有图的题解，那我就过来补个图加思路了

画图

假设我们有一颗树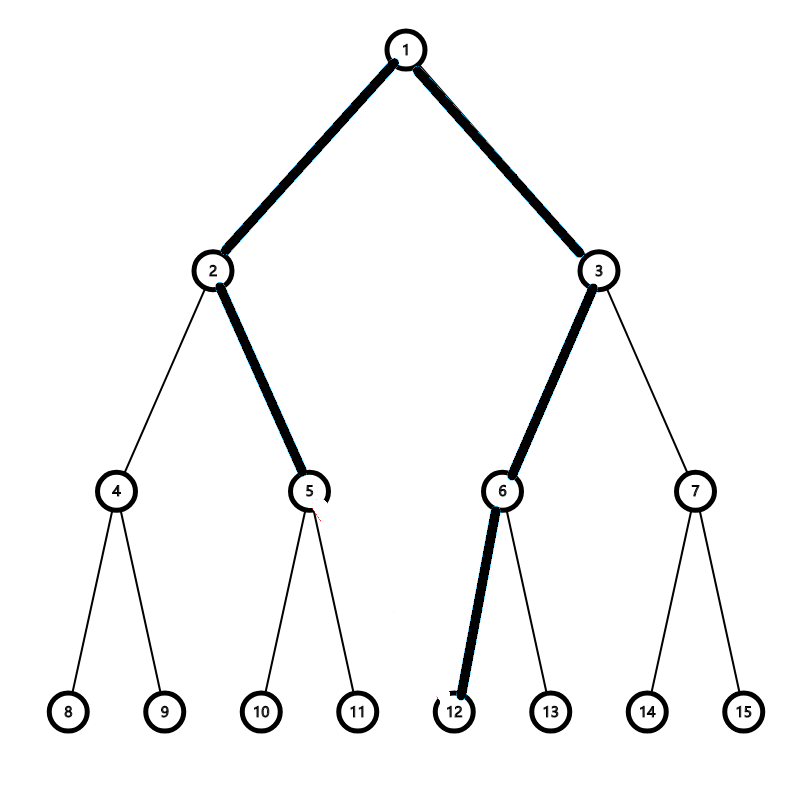

现在多了一条额外道路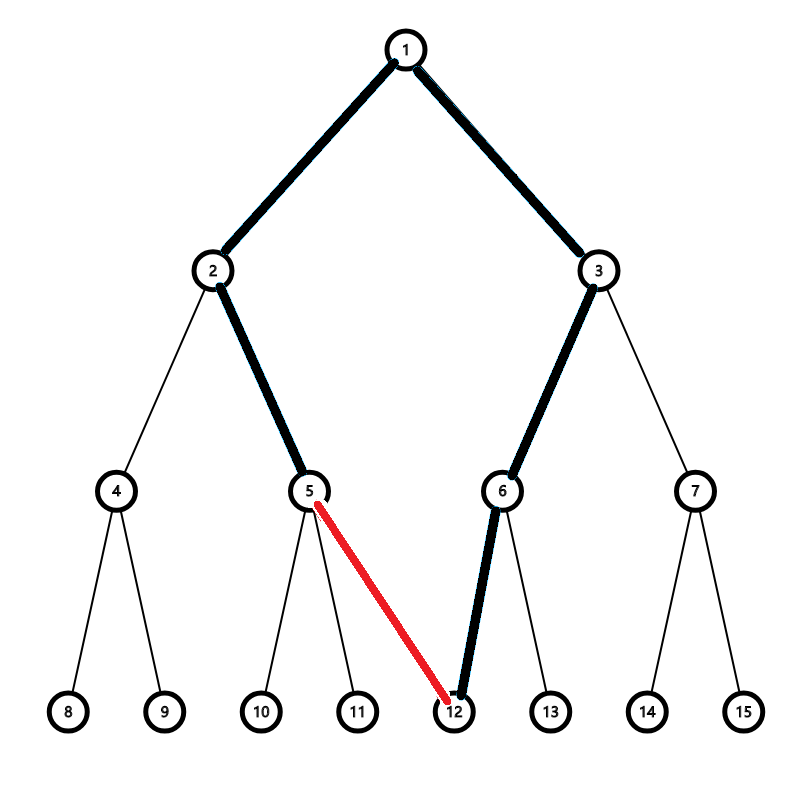

则当且仅当额外道路所连的两个点不在一个联通块内时，这条边才有贡献，我们将能够将这两个点分开的边标记出来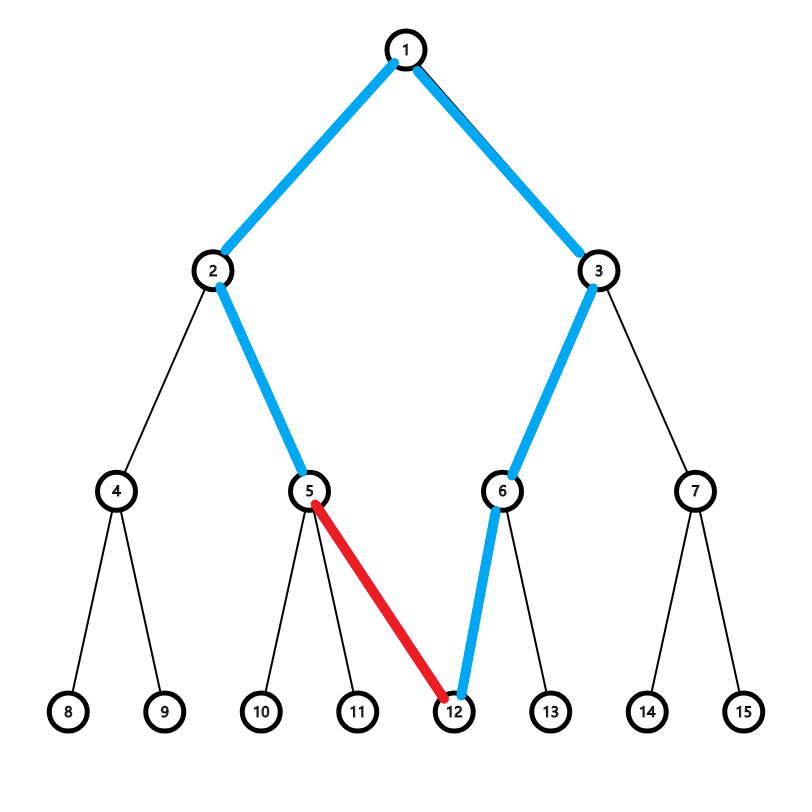

发现这些边构成的路径就是两点之间的最短简单路径，直接用树剖维护区间极值即可
（不要问我前两张图为什么那么怪，因为我是由结果改出过程（简称懒））

证明

两点不在同一个联通快内，即两点之间不存在简单路径，因为这是一棵树，所以两点之间的简单路径是唯一的，只有切断简单路径才能使两个点不在一个联通块内，证毕

代码

#include <bits/stdc++.h>
using namespace std;
const int N=50009;
int head[N],to[N<<1],nt[N<<1];
struct gzw
{
    int st,ed,val;
}way[N];
int n,m,bh,totid;
int top[N],siz[N],mxson[N],fa[N],dep[N],id[N];
int u[N],v[N];
int val[N<<4],tag[N<<4];
bool rnk(gzw a,gzw b)
{
    return a.val>b.val;    
}
void add(int u,int v)
{
    bh++;
    nt[bh]=head[u];
    head[u]=bh;
    to[bh]=v;
}
void dfs1(int now,int fath,int depth)
{
    fa[now]=fath;
    dep[now]=depth;
    siz[now]=1;
    for(int i=head[now],mx=0;i;i=nt[i])
    {
        if(to[i]!=fath)
        {
            dfs1(to[i],now,depth+1);
            siz[now]+=siz[to[i]];
            if(siz[to[i]]>mx) mx=siz[to[i]],mxson[now]=to[i];    
        }
    }
}
void dfs2(int now,int tp)
{
    id[now]=++totid;
    top[now]=tp;
    if(mxson[now])
    {
        dfs2(mxson[now],tp);
    }
    for(int i=head[now];i;i=nt[i])
    {
        if(to[i]!=fa[now]&&to[i]!=mxson[now])
        {
            //cout<<now<<" "<<to[i]<<endl;
            dfs2(to[i],to[i]);
        }
    }
}
void upd (int &x,int k)
{
    x=(x==-1?k:min(x,k));    
}
void pushdown(int now)
{
    if(tag[now]!=-1)
    {
        upd(val[now],tag[now]);
        upd(tag[now<<1],tag[now]);
        upd(tag[now<<1|1],tag[now]);
        tag[now]=-1;
    }
}
int query(int now,int l,int r,int pos)
{
    //cout<<l<<" "<<r<<" "<<pos<<endl;
    pushdown(now);
    if(l==pos&&r==pos)
    {
        return val[now];
    }
    int mid=(l+r)>>1;
    if(mid>=pos) query(now<<1,l,mid,pos);
    else query(now<<1|1,mid+1,r,pos);
}
void change(int now,int l,int r,int ql,int qr,int k)
{
    pushdown(now);
    if(ql<=l&&qr>=r)
    {
        //cout<<now<<" "<<ql<<" "<<qr<<" "<<l<<" "<<r<<" 666"<<endl;
        upd(val[now],k);
        upd(tag[now<<1],k);
        upd(tag[now<<1|1],k);
        return;
    }
    int mid=(l+r)>>1;
    if(mid>=qr) change(now<<1,l,mid,ql,qr,k);
    else if(mid<ql) change(now<<1|1,mid+1,r,ql,qr,k);
    else change(now<<1,l,mid,ql,qr,k),change(now<<1|1,mid+1,r,ql,qr,k);
    return;
}
void C(int x,int y,int k)
{
    int tx=top[x],ty=top[y];
    while(tx!=ty)
    {
        if(dep[tx]<dep[ty]) swap(x,y),swap(tx,ty);
        //cout<<id[tx]<<" "<<id[x]<<" "<<k<<" 233"<<endl;
        change(1,1,n,id[tx],id[x],k);
        x=fa[tx],tx=top[x];
    }
    if(x!=y) 
    {
        if(id[x]>id[y]) swap(x,y);
        //cout<<id[x]+1<<" "<<id[y]<<" "<<k<<" 233"<<endl;
        change(1,1,n,id[x]+1,id[y],k);//???
    }
}
void bl(int now,int l,int r)
{
    pushdown(now);
    //cout<<now<<" "<<l<<" "<<r<<" "<<val[now]<<endl;
    if(l>=r) return;    
    bl(now<<1,l,(l+r)>>1);
    bl(now<<1|1,((l+r)>>1)+1,r);
}
int main() 
{
    scanf("%d %d",&n,&m);
    for(int i=1;i<n;i++)
    {
        scanf("%d %d",&u[i],&v[i]);
        add(u[i],v[i]);
        add(v[i],u[i]);
    }
    for(int i=1;i<=m;i++)
    {
        scanf("%d %d %d",&way[i].st,&way[i].ed,&way[i].val);    
    }
    sort(way+1,way+m+1,rnk);
    dfs1(1,0,1);
    dfs2(1,1);

    memset(val,-1,sizeof(val));
    memset(tag,-1,sizeof(tag));
    for(int i=1;i<=m;i++)
    {
        C(way[i].st,way[i].ed,way[i].val);    
        //bl(1,1,n);
        //cout<<endl;
    }
    for(int i=1,ls;i<n;i++)
    {
        //cout<<(dep[u[i]]>dep[v[i]]?id[u[i]]:id[v[i]])<<" "<<666<<endl;
        ls=query(1,1,n,dep[u[i]]>dep[v[i]]?id[u[i]]:id[v[i]]);
        printf("%d\n",ls);
    }
}
/*

*/